🪴 Obsidian Publish

Leetcode算法 - 动态规划

5分钟阅读

状态压缩 DP

6007. 数组的最大与和 - 力扣（LeetCode）
Notion – The all-in-one workspace for your notes, tasks, wikis, and databases.
状态定义：
使用 0-1 标志篮子是否被占用，篮子有 m 个，则有 2^m 个状态。使用 dp[state]标志该状态下的最大值。
state 时，有 k 个篮子被占用，则表明有 k 个数组元素已经被使用了，定义 dp[state]为前 k 个数组元素被使用后的最大值。
转移方程：
在 state 的基础上，使用第 k 个数组元素，将其安排到篮子里。
具体为，计算 k，即当前要使用的数组元素，然后遍历所有篮子，将其放到篮子里。

if state&(1<<j) == 0: # 当前篮子是空的
	newstate = state | (1<<j) # 新的状态
	dp[newstate] = max(dp[newstate], dp[state]+第 k 个数组放到第 j 个篮子里的 value)

完整代码：

class Solution {
    public int maximumANDSum(int[] nums, int numSlots) {
        var ans = 0;
        var dp = new int[1 << (numSlots * 2)];  # 所有的状态
        for (var i = 0; i < dp.length; i++) {
            var c = Integer.bitCount(i);   # 第 k 个元素
            if (c >= nums.length) continue;
            for (var j = 0; j < numSlots * 2; ++j) {  # 遍历所有篮子，计算放入当前篮子后的状态
                if ((i & (1 << j)) == 0) {
                    var s = i | (1 << j);
                    dp[s] = Math.max(dp[s], dp[i] + ((j / 2 + 1) & nums[c]));
                    ans = Math.max(ans, dp[s]);
                }
            }
        }
        return ans;
    }
}

847. 访问所有节点的最短路径 - 力扣（LeetCode）
状态定义：
使用 0-1 标志每个节点是否被访问过，同时需要记录访问后的终点，以便作为下一条的起点。
因此定义状态数组 dp[1<<n][n]
状态转移：
当前处于 dp[state][i] 状态，那么对于 i 节点到 j 节点的状态转移为：
dp[state|(1<<j)][j] = min(dp[state][i]+1, dp[state|(1<<j)][j])
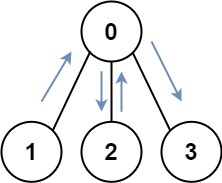
然而，这里有个坑，那就是可能当存在访问到 state 状态时，并非所有 state 状态的所有访问节点的出状态已经就位了。
例如下图，当开始 state=(111)2 遍历的时候，dp[state][0] 状态其实是没有准备好的，即最大值，因为它需要从 dp[state][1] 状态从 1 节点去往 0 节点。这时候，从 0 节点前往 3 节点的时候，获得的是最大值，并非实际的 4 值。所以，需要两遍转移。

其他：
1 - 也可以使用 Floyd 算法先计算出每个节点之间的距离，然后从所有已访问节点转移到未访问节点就可以了。
2 - 使用单端队列，从所有节点出发，然后使用状态数组记录状态。

    public int shortestPathLength(int[][] graph) {
        int n = graph.length;
        if(n <= 1) return 0;
        int state = 1 << n;
        int dp[][] = new int[state][n];
        for(int i = 1; i < state; i++){
            Arrays.fill(dp[i], 100000);
        }
        for(int i = 0; i < state; i++){
            for(int j = 0; j < n; j++){
                for(int next: graph[j]){
                    dp[i|(1<<next)][next] = Math.min(dp[i|(1<<next)][next], dp[i][j]+1);
                }
            }
            for(int j = 0; j < n; j++){
                for(int next: graph[j]){
                    dp[i|(1<<next)][next] = Math.min(dp[i|(1<<next)][next], dp[i][j]+1);
                }
            }
        }
        int res = 1000000;
        for(int i = 0; i < n; i++){
            res = Math.min(dp[(1<<n)-1][i], res);
        }
        return res-1;
    }

子集动态规划

1595. 连通两组点的最小成本
1986. 完成任务的最少工作时间段
1494. 并行课程 II
1655. 分配重复整数

for(int i = 0; i < nn; i++)
	cost[i] = cost[i&(i-1)] + cost[Integer.heghestOneBit(i&(-i))-1];
	// i&(i-1) 去掉二进制最后一个1
	// i&(-i) 表示2^k，其中k表示i中从低位到高位的第一个1的位索引
for(int i = 1; i < nn; i++) g[i] = g[i&(i-1)]+cost[__lg(i&(-1))]
for state in range(1, nn): state_cnt[state] = state_cnt[state&(state-1)] + cost[int(math.log(state&(-state), 2))]

反向链接